�J���o�ϊw���@����
�P�D�����i���̌v��
�@�Љ�̍\�������R�l�ȏ�̂Ƃ��̏����i���͗e�Ղɂ͌v���ł��Ȃ��B
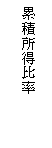
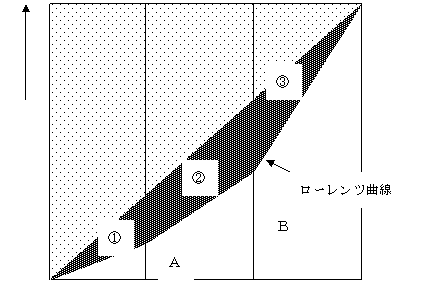
�W�j�W���ƃ��[�����c�Ȑ�
![]()
�@�W�j�W���̓��[�����c�Ȑ��ƂS�T�x�����͂ޖʐς̂Q�{�B�Љ�̍\�������R�l�ŁA�ݐϏ����䗦���`�C�a�C�b���Ƃ���ƁA�@�`�B�̖ʐς͈ȉ��̂Ƃ���ƂȂ�B
�@�i(1/3)�|�`�j�~(1/3)���Q���i1/18�j�|(1/6)�`
�A�i(1/3)�|�`�{(2/3)�|�a�j�~(1/3)���Q��(1/6)�|(1/6)�i�`�{�a�j
�B�i(2/3)�|�a�j�~(1/3)���Q���i1/�X�j�|(1/6)�a
�@�`�B�̍��v�́@(1/3)�|(1/3)�`�|(1/3)�a��(1/3)�i�P�|�`�|�a�j
����̂Q�{���W�j�W��
�Ⴆ�Ώ������A�P�l�ځF�Q�A�Q�l�ځF�R�A�R�l�ځF�T�@�������Ɖ��肷��ƁA�ݐϏ����䗦�͂`��0.2�A�a��0.5
������W�j�W���́@�Q�~(1/3)�i�P�|0.2�|0.5�j��2/3*0.3���O�D�Q�ƂȂ�B
��ʉ����ꂽ�W�j�W���iGini coefficient�j
�@�������z�̕s�����x�𑪂�w�W�B�c���ɗݐϏ����̕S����C�����ɗݐϐl���̕S������Ƃ�Ƃ��C�Ίp���͕��z�̊��S�����������C�����̕��z�͑Ίp�������Ƃ���|�`�̋Ȑ��Ŏ������B��������[�����c�Ȑ��Ƃ����C�W�j�W���̓��[�����c�Ȑ��ƑΊp���ň͂܂ꂽ�����̖ʐς̂Q�{�ƂȂ�B
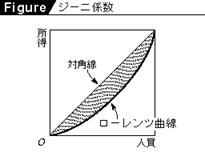
���� yi
�������̒Ⴂ����(y1�Cy2�C�c�c�Cyn)�ŗ^�����Ă���Ƃ��C�W�j�W�� G ��
�f����������i�|������/�Q�ʂ�2
�@�@��
��
�Œ�`���ꂽ�l�ł���B���Ȃ킿�W�j�W���Ƃ́C�����̑g����(yi�Cyj)�����ׂĂ̍\�����ɂ��čl���C���̍�(��Βl)�̕��ϊz�Ϗ��� �� �ŏ������l�̔����ł���B�����ɂ���̂́C�����̃y�A(yi�Cyj)��(yj�Cyi)�̏��������o���Ƃ��ɍl������Ă��邩��ɂق��Ȃ�Ȃ��B���������āC���Ƃ��W�j�W����0.4�ɓ������Ƃ��C�C�ӂɑI�тƂ���
2�l�̊Ԃ̏������͑S�̂Ƃ��Ă݂�Ε��Ϗ�����40���ɑ������Ă��邱�ƂɂȂ�B�W�j�W���͊��S�����̂Ƃ��ŏ��l0���Ƃ�C������1�l�ɏW�����Ă��銮�S�s�����̂Ƃ��ő�l(1�|1/n)���Ƃ�B
�@�W�j�W���̓��[�����c�Ȑ���p���Đ}���\�ł���B���Ȃ킿�ϓ����z��(�Ίp��)�ƃ��[�����c�Ȑ��ň͂܂ꂽ���`�̖ʐς�2�{�ɃW�j�W���͓������B�Ȃ����[�����c�Ȑ�����������ꍇ�C�W�j�W���Ƃ͈قȂ�s�����̏����Â������̎w�W(���Ƃ��Εϓ��W���C����͕W�����Ϗ����ŏ������l)��p����Ɖ\�ł���B���̎w�W�Ɣ�r����ƁC�W�j�W���͒��ԏ����K�w�̏����̓����ɍł��q���ł��邱�Ƃ��m���Ă���B
��L�̗�i�������Q�C�R�C�T�̂R�l�ō\�������Љ�̃W�j�W������̎��Ōv�Z�����
|
�@ |
1 |
2 |
3 |
���v |
|
1 |
0 |
1 |
3 |
4 |
|
2 |
1 |
0 |
2 |
3 |
|
3 |
3 |
2 |
0 |
5 |
|
���v |
4 |
3 |
5 |
12 |
|
|
|
|
|
|
|
���� |
3.333333 |
|
|
|
|
�W�j�W�� |
0.2 |
|
|
|
���������ʂ͂O�D�Q�ƂȂ�B
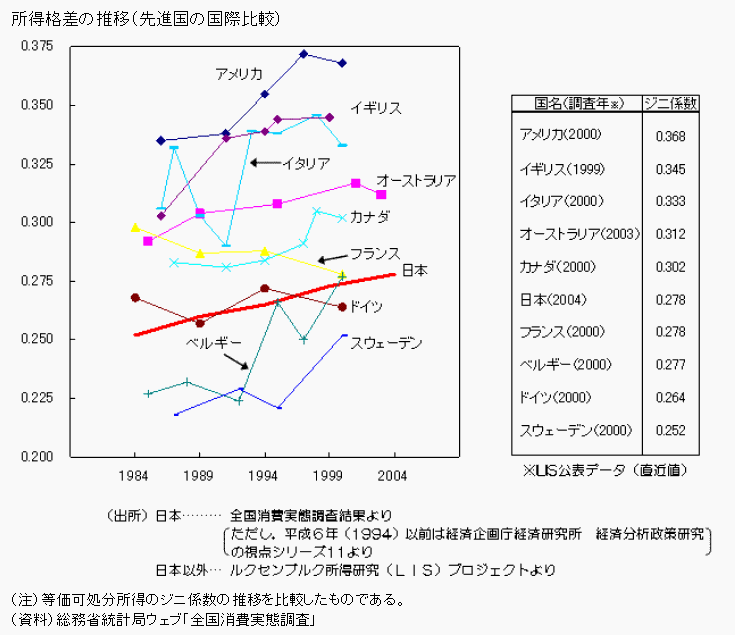
(�o��)�Љ����f�[�^�}�^�@
http://www2.ttcn.ne.jp/~honkawa/4660.html